Why perceptron is not suitable for handling XOR problems? How can the XOR problem be solved?
Perceptron is only capable of learning linearly separable data which means the data can be separated by a single line. Since the XOR function is not linearly separable Perceptron cannot be used to learn it. From the given truth table, we can see why XOR isn’t linearly separable.
| x | y | XY= x^y+y^x |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |

As we can see there is no way to separate the output values from a single line. This is because the output values are not linearly related to output values.
The XOR problem can be solved by using Multi-Layer Perceptron with an input layer, hidden layer, and output layer. In this way when there is forward propagation through neural networks, the weight gets updated to the corresponding layer executing the XOR Logic.
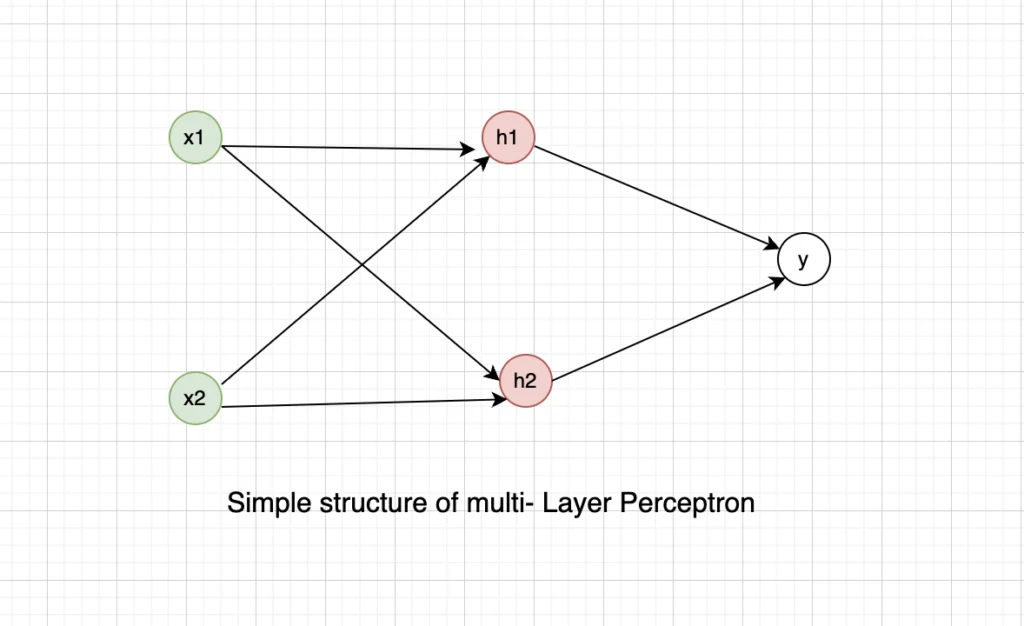
It’s important to note that the input layer is the first one in this particular architecture. The second layer (hidden layer) changes the initial non-linearly separable problem into a linearly separable one, which the third layer (output layer) can subsequently solve.
Solving the XOR problem with a neural network
The following is a snippet of Python code that use the Keras package to build a multi-layer perceptron to perform the XOR operation:
# Import the necessary libraries
import numpy as np
from keras.models import Sequential
from keras.layers import Dense
# Define the XOR input data
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
# Define the corresponding XOR output data
y = np.array([0, 1, 1, 0])
# Create a sequential model
model = Sequential()
# Add a hidden layer with two neurons and a ReLU activation function
model.add(Dense(2, input_dim=2, activation='relu'))
# Add an output layer with one neuron and a sigmoid activation function
model.add(Dense(1, activation='sigmoid'))
# Compile the model
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# Train the model
model.fit(X, y, epochs=5000, verbose=0)
# Evaluate the model
loss, accuracy = model.evaluate(X, y)
print(f"Loss: {loss}, Accuracy: {accuracy}")
# Predict the XOR outputs
predictions = model.predict(X)
for i in range(4):
print(f"Input: {X[i]}, Predicted Output: {round(predictions[i][0])}")1/1 [==============================] - 0s 175ms/step - loss: 0.4805 - accuracy: 0.7500
Loss: 0.48054248094558716, Accuracy: 0.75
1/1 [==============================] - 0s 80ms/step
Input: [0 0], Predicted Output: 1
Input: [0 1], Predicted Output: 1
Input: [1 0], Predicted Output: 1
Input: [1 1], Predicted Output: 0We hope this article on helped our readers to understand Why can’t the XOR-problem be solved by a one-layer perceptron? You can also read our articles on What may happen if you set the momentum hyperparameter too close to 1 (e.g., 0.99999) when using an SGD optimizer?
